7 एल्गोरिदम हर प्रोग्रामर को पता होना चाहिए

प्रोग्रामिंग के एक छात्र के रूप में, आपने अपने करियर के दौरान बहुत सारे अलग-अलग एल्गोरिदम सीखे हैं। विभिन्न एल्गोरिदम में कुशल बनना किसी भी प्रोग्रामर के लिए नितांत आवश्यक है।

इतने सारे एल्गोरिदम के साथ, जो आवश्यक है उसका ट्रैक रखना चुनौतीपूर्ण हो सकता है। यदि आप एक साक्षात्कार के लिए तैयारी कर रहे हैं या बस अपने कौशल पर ब्रश कर रहे हैं, तो यह सूची अपेक्षाकृत आसान बना देगी। आगे पढ़ें क्योंकि हम प्रोग्रामर के लिए सबसे आवश्यक एल्गोरिदम को सूचीबद्ध करते हैं।

1. दिज्क्स्ट्रा का एल्गोरिथम

Edsger Dijkstra अपने समय के सबसे प्रभावशाली कंप्यूटर वैज्ञानिकों में से एक थे, और उन्होंने इसमें योगदान दिया कंप्यूटिंग विज्ञान के कई अलग-अलग क्षेत्र, जिनमें ऑपरेटिंग सिस्टम, कंपाइलर निर्माण, और बहुत कुछ शामिल हैं अधिक। दिज्क्स्ट्रा के सबसे उल्लेखनीय योगदानों में से एक ग्राफ के लिए उनके सबसे छोटे पथ एल्गोरिदम की सरलता है, जिसे डिजस्ट्रा के सबसे छोटे पथ एल्गोरिदम के रूप में भी जाना जाता है।

दिज्क्स्ट्रा का एल्गोरिथ्म एक स्रोत से सभी ग्राफ़ शीर्षों तक ग्राफ़ में एकल सबसे छोटा पथ ढूंढता है। एल्गोरिथ्म के प्रत्येक पुनरावृत्ति पर, स्रोत से न्यूनतम दूरी के साथ एक शीर्ष जोड़ा जाता है और एक जो वर्तमान सबसे छोटे पथ में मौजूद नहीं है। यह जिक्स्ट्रा के एल्गोरिथम द्वारा उपयोग की जाने वाली लालची संपत्ति है।

एल्गोरिथ्म आमतौर पर एक सेट का उपयोग करके लागू किया जाता है। मिन हीप के साथ कार्यान्वित होने पर दिज्क्स्ट्रा का एल्गोरिथ्म बहुत कुशल है; आप केवल O(V+ElogV) समय में सबसे छोटा पथ पा सकते हैं (V शीर्षों की संख्या है और E किसी दिए गए ग्राफ़ में किनारों की संख्या है)।

दिज्क्स्ट्रा के एल्गोरिथ्म की अपनी सीमाएँ हैं; यह केवल निर्देशित और अप्रत्यक्ष ग्राफ़ पर सकारात्मक भार के किनारों के साथ काम करता है। नकारात्मक भार के लिए, बेलमैन-फोर्ड एल्गोरिथम आमतौर पर बेहतर होता है।

साक्षात्कार के प्रश्नों में आमतौर पर जिक्स्ट्रा का एल्गोरिथम शामिल होता है, इसलिए हम इसके जटिल विवरण और अनुप्रयोगों को समझने की अत्यधिक अनुशंसा करते हैं।

2. मर्ज़ सॉर्ट

इस सूची में हमारे पास कुछ सॉर्टिंग एल्गोरिदम हैं, और मर्ज सॉर्ट सबसे महत्वपूर्ण एल्गोरिदम में से एक है। यह फूट डालो और जीतो प्रोग्रामिंग तकनीक पर आधारित एक कुशल छँटाई एल्गोरिथ्म है। सबसे खराब स्थिति में, मर्ज सॉर्ट केवल O (nlogn) समय में "n" संख्याओं को सॉर्ट कर सकता है। आदिम छँटाई तकनीकों की तुलना में जैसे बबल शॅाट (जिसमें ओ (एन ^ 2) समय लगता है), मर्ज सॉर्ट उत्कृष्ट रूप से कुशल है।

सम्बंधित: मर्ज सॉर्ट एल्गोरिथम का परिचय

मर्ज सॉर्ट में, सॉर्ट किए जाने वाले ऐरे को बार-बार सबएरे में तोड़ा जाता है जब तक कि प्रत्येक सबअरे में एक ही नंबर न हो। पुनरावर्ती एल्गोरिथ्म फिर बार-बार उप-सरणी को मिलाता है और सरणी को सॉर्ट करता है।

3. जल्दी से सुलझाएं

क्विक्सोर्ट डिवाइड एंड कॉनकर प्रोग्रामिंग तकनीक पर आधारित एक और सॉर्टिंग एल्गोरिदम है। इस एल्गोरिथम में, एक तत्व को पहले पिवट के रूप में चुना जाता है, और फिर पूरे ऐरे को इस पिवट के चारों ओर विभाजित किया जाता है।

जैसा कि आपने शायद अनुमान लगाया है, एक कुशल प्रकार के लिए एक अच्छा धुरी महत्वपूर्ण है। धुरी या तो एक यादृच्छिक तत्व, मीडिया तत्व, पहला तत्व या अंतिम तत्व भी हो सकता है।

क्विकॉर्ट का कार्यान्वयन अक्सर उनके द्वारा पिवट चुनने के तरीके में भिन्न होता है। औसत स्थिति में, Quicksort केवल O(nlogn) समय में एक अच्छी धुरी के साथ एक बड़ी सरणी को सॉर्ट करेगा।

क्विकॉर्ट का सामान्य छद्म कोड बार-बार पिवट पर सरणी को विभाजित करता है और इसे सबएरे की सही स्थिति में रखता है। यह धुरी से छोटे तत्वों को अपनी बाईं ओर और धुरी से बड़े तत्वों को इसके दाईं ओर रखता है।

4. गहराई पहली खोज

डेप्थ फर्स्ट सर्च (डीएफएस) छात्रों को पढ़ाए जाने वाले पहले ग्राफ एल्गोरिदम में से एक है। DFS एक कुशल एल्गोरिथम है जिसका उपयोग ग्राफ़ को पार करने या खोजने के लिए किया जाता है। इसे ट्री ट्रैवर्सल में उपयोग करने के लिए संशोधित भी किया जा सकता है।

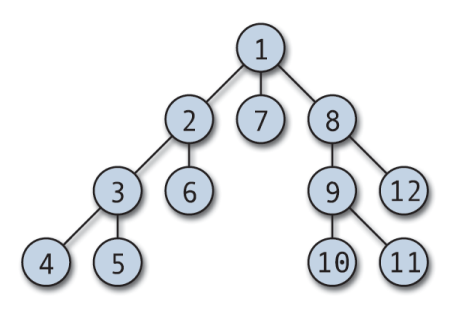
DFS ट्रैवर्सल किसी भी मनमाने नोड से शुरू हो सकता है, और यह प्रत्येक आसन्न शीर्ष में गोता लगाता है। एल्गोरिथम बैकट्रैक तब होता है जब कोई अनविजिटेड वर्टेक्स नहीं होता है, या कोई डेड-एंड होता है। डीएफएस आमतौर पर विज़िट किए गए नोड्स का ट्रैक रखने के लिए स्टैक और बूलियन सरणी के साथ कार्यान्वित किया जाता है। डीएफएस को लागू करना आसान है और असाधारण रूप से कुशल है; यह (V+E) काम करता है, जहां V शीर्षों की संख्या है और E किनारों की संख्या है।

डीएफएस ट्रैवर्सल के विशिष्ट अनुप्रयोगों में टोपोलॉजिकल सॉर्ट, ग्राफ में चक्रों का पता लगाना, पथ-खोज और दृढ़ता से जुड़े घटकों को ढूंढना शामिल है।

5. पहले चौड़ाई खोजो

चौड़ाई-पहली खोज (बीएफएस) को पेड़ों के लिए एक स्तरीय ऑर्डर ट्रैवर्सल के रूप में भी जाना जाता है। BFS DFS एल्गोरिथम के समान O(V+E) में कार्य करता है। हालाँकि, BFS स्टैक के बजाय एक कतार का उपयोग करता है। DFS ग्राफ़ में गोता लगाता है, जबकि BFS ग्राफ़ को चौड़ाई में घुमाता है।

बीएफएस एल्गोरिथ्म कोने का ट्रैक रखने के लिए एक कतार का उपयोग करता है। अनदेखी आसन्न कोने का दौरा किया जाता है, चिह्नित किया जाता है, और कतारबद्ध किया जाता है। यदि शीर्ष में कोई आसन्न शीर्ष नहीं है, तो एक शीर्ष को कतार से हटा दिया जाता है और उसका पता लगाया जाता है।

बीएफएस आमतौर पर पीयर-टू-पीयर नेटवर्क में उपयोग किया जाता है, बिना भारित ग्राफ का सबसे छोटा पथ, और न्यूनतम फैले हुए पेड़ को खोजने के लिए।

6. द्विआधारी खोज

द्विआधारी खोज एक क्रमबद्ध सरणी में आवश्यक तत्व को खोजने के लिए एक सरल एल्गोरिथ्म है। यह सरणी को बार-बार आधे में विभाजित करके काम करता है। यदि आवश्यक तत्व मध्य तत्व से छोटा है, तो मध्य तत्व के बाईं ओर आगे संसाधित किया जाता है; अन्यथा, दाईं ओर आधा कर दिया जाता है और फिर से खोजा जाता है। आवश्यक तत्व मिलने तक प्रक्रिया को दोहराया जाता है।

द्विआधारी खोज की सबसे खराब स्थिति समय जटिलता ओ (लॉगन) है जो इसे रैखिक सरणी खोजने में बहुत कुशल बनाती है।

7. न्यूनतम स्पैनिंग ट्री एल्गोरिदम

ग्राफ़ के न्यूनतम फैले हुए पेड़ (MST) की सभी संभावित फैले हुए पेड़ों में न्यूनतम लागत होती है। एक फैले हुए पेड़ की कीमत उसके किनारों के वजन पर निर्भर करती है। यह ध्यान रखना महत्वपूर्ण है कि एक से अधिक न्यूनतम फैले हुए पेड़ हो सकते हैं। दो मुख्य एमएसटी एल्गोरिदम हैं, अर्थात् क्रुस्कल और प्राइम।

क्रुस्कल का एल्गोरिथ्म बढ़ते हुए सेट में न्यूनतम लागत के साथ बढ़त जोड़कर एमएसटी बनाता है। एल्गोरिथम पहले किनारों को उनके वजन के आधार पर छांटता है और फिर किनारों को न्यूनतम से शुरू करते हुए एमएसटी में जोड़ता है।

यह ध्यान रखना महत्वपूर्ण है कि एल्गोरिथ्म एक चक्र बनाने वाले किनारों को नहीं जोड़ता है। विरल रेखांकन के लिए क्रुस्कल का एल्गोरिथ्म पसंद किया जाता है।

प्राइम का एल्गोरिदम भी लालची संपत्ति का उपयोग करता है और घने रेखांकन के लिए आदर्श है। प्राइम के एमएसटी में केंद्रीय विचार दो अलग-अलग सेटों के शिखर होना है; एक सेट में बढ़ते एमएसटी होते हैं, जबकि दूसरे में अप्रयुक्त शिखर होते हैं। प्रत्येक पुनरावृत्ति पर, दो सेटों को जोड़ने वाला न्यूनतम वजन किनारा चुना जाता है।

क्लस्टर विश्लेषण, वर्गीकरण और प्रसारण नेटवर्क के लिए न्यूनतम फैले हुए ट्री एल्गोरिदम आवश्यक हैं।

एक कुशल प्रोग्रामर एल्गोरिदम के साथ कुशल है

प्रोग्रामर लगातार अपने कौशल को सीखते और विकसित करते हैं, और कुछ मूल अनिवार्यताएं हैं जिनमें सभी को कुशल होने की आवश्यकता होती है। एक कुशल प्रोग्रामर विभिन्न एल्गोरिदम, प्रत्येक के लाभ और कमियों को जानता है, और किसी दिए गए परिदृश्य के लिए कौन सा एल्गोरिदम सबसे उपयुक्त होगा।

शेल सॉर्ट एल्गोरिथम का परिचय

जबकि शेल सॉर्ट सबसे कुशल तरीका नहीं है, शुरुआती लोगों को इसका अभ्यास करने से बहुत कुछ हासिल होता है।

आगे पढ़िए

लेखक के बारे में